We examine the currently proposed static and dynamic graph watermarking schemes. Graph based watermarking schemes, like other watermarking schemes, can be divided into two groups: static and dynamic. Static graph watermarks are embedding in a control-flow graph within a program whereas dynamic graph watermarks are embedding in a graph data-structure built at run-time. We report previous findings, describe some recent additions and conclude by suggesting a direction for future work.

The full paper is summarised on this page; the full paper contains more details and examples.

Encoding Watermarks in Graphs

Collberg et al.1 describe several techniques for encoding watermark integers in graph structures. The algorithms in this paper rely on the fact that graph-generating code is difficult to analyse due to aliasing effects 2 which, in general, is known to be un-decidable 3.

An ideal class of watermarking graph should have the following properties 4:

• ability to efficiently encode a watermark integer; and be efficiently decodable to a watermark integer
• a root node from which all other nodes are reachable
• a high data-rate
• a low outdegree to resemble common data structures such as lists and trees
• error correcting properties to allow detection after transformation attacks
• tamper-proofing abilities
• have some computationally feasible algorithms for graph isomorphism, for use during recognition

Graph Enumeration

The family of graph encoding is based on a branch of graph theory known as graphical enumerations5. An integer watermark \(n\) is encoded as the \(n^{th}\) enumeration of a given graph.

Directed Parent-Pointer Trees

This family of graphs contains a single edge between a vertex and it's parent. For example, there are 4 possible enumerations of DPPTs having four indistinguishable vertices6. We choose the n^th enumerated graph to embed the watermark number n. Implementing a parent-pointer tree data-structure is space efficient because each node has just one pointer field referencing it's parent. However, the data-structure is fragile and an adversary could add a single node or edge to distort the watermark.

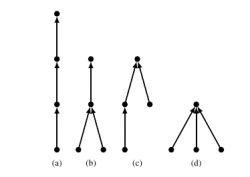
Planted Planar Cubic Trees

Planted planar cubic trees (PPCT) are binary trees where every interior vertex, except the root, has two children. These are easily enumerated by using a Catalan recurrence7 8. The Catalan number c(n) gives the number of unique trees for each n. An integer is encoded as one of the trees.

PPCTs can be made more resilient to attacks by a) marking each leaf with a self-pointer, and b) creating an outer cycle from the root to itself through all the leaves9. This allows single edge and node insertions to be detected; however, multiple changes cannot be detected or corrected. The PPCT graphs have a lower bit-rate than other graph families but are more resilient to attacks.

Radix Graphs

Radix graphs add an extra pointer field in each vertex of a circular linked list of length k to encode a base-k digit. It is possible to encode watermark digits where a self-pointer represents 0, a pointer to the next node 1, and so on.

These graphs give the highest data-rate for encoding watermarks however they are fragile as the watermark could easily be distorted. We can add redundancy to these watermarks by restricting the indegree to two and outdegree to two and using a permutation graph 1.

Several papers10 11 12 13 14 15 describe a technique which combines radix graphs with the error-correcting properties of PPCTs by converting a radix graph into a PPCT-like structure.

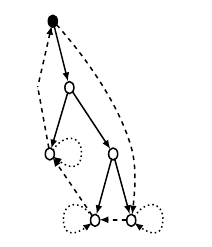
Permutation Graphs

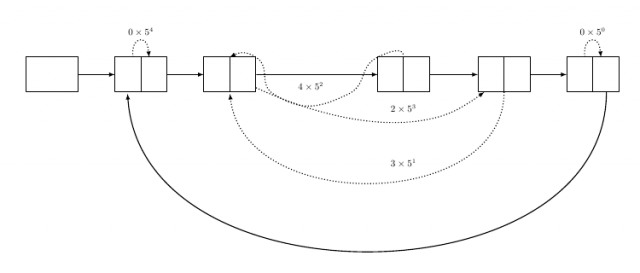
Permutation based graphs (as defined by Collberg et al.1) use the same basic singly linked circular list structure as the radix graphs but have error-correcting properties. In this encoding scheme a permutation P = {p₁, p₂, ..., p_n} is derived from the watermark integer n; the permutation is then encoded in the graph by adding edges between vertices i and p_i.

Collberg and Nagra9 give algorithms for encoding and decoding an integer as a permutation. For example, the integer 97₁₀ is encoded as the permutation {3, 1, 0, 2, 4}.

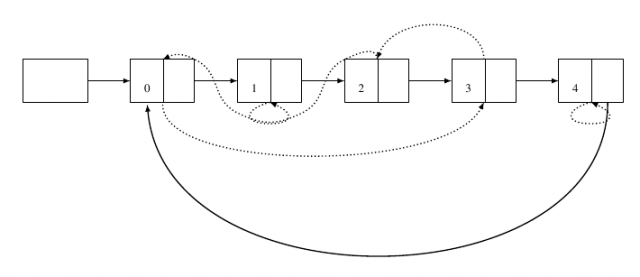
If an adversary changes one of the non-spine pointers to point to a different vertex we will discover an error because the permutation graph encodes a unique permutation - each vertex must have indegree two. However, if the adversary swaps two pointers we will lose the watermark.

Reducible Permutation Graphs

Reducible permutation graphs (RPG)16 17 are very similar to permutation graphs but they closely resemble control-flow graphs18 as they are reducible-flow graphs19 20.

The reducibility of this family of graphs means that they resemble control-flow graphs constructed from programming constructs such as if, while etc.9.

RPGs, like CFGs, contain a unique entry node and a unique exit node, a preamble which contains zero or more nodes from which all other nodes can be reached and a body which encodes a watermarking using a self-inverting permutation21.

Static Graph Watermarking

Venkatesan et al.16 proposed the first static graph watermarking scheme, Graph Theoretic Watermarking (GTW), which encodes a value in the topology of a program's control-flow graph18. The idea was later patented by Venkatesan et al.17 for Microsoft. The basic concept is to encode a watermark value in a reducible permutation graph and convert it into a control flow graph; it is then merged with the program control flow graph by adding control flow edges between the two.

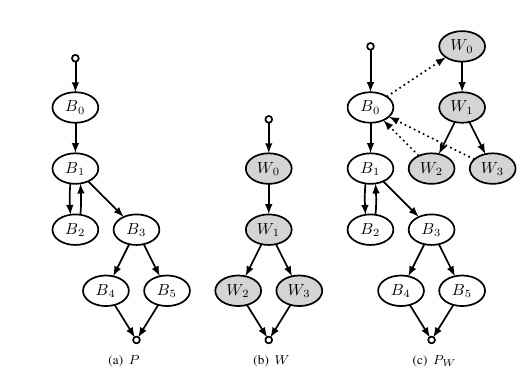
The algorithm adds bogus control flow edges between random pairs of vertices in the program CFG and watermark CFG in order to protect against static analysis attacks looking for sparse-cuts22 in the control-flow graph. A sparse-cut would indicate a possible joining point of the original program CFG and the watermark CFG where the attacker could split the program with as few edges broken as possible. For example, we could insert a call to the sum, or any other method in the original program, in the watermark method. The GTW algorithm also inserts bogus method calls in between parts of the original program so that the location of bogus calls cannot be used to point out the location of the watermark.

In order to recognise a GTW we must know which basic blocks, from the program's CFG, are part of the watermark graph; we must therefore mark the watermark basic blocks in some way in order to identify them. We could, for example, re-order instructions such that they are in lexicographic order, or insert bogus instructions to identify a watermark basic block9. However, these techniques are not resilient to semantics-preserving transformations and an attacker could remove the marks so that we cannot mark our watermark blocks.

Collberg et al.23 implemented a version GTW_SM of GTW in Sandmark24 in order to evaluate the algorithm. They measured the size and time overhead of watermarking and evaluated the algorithm against a variety of attacks. They also introduce two methods (Partial Sum splitting and Generalised Chinese Remainder Theorem25 splitting) for splitting a watermark integer into redundant pieces so that a large integer can be stored in several smaller CFGs. They found that stealth is a big problem; for example, the basic blocks of the generated watermark method consisted of 20% arithmetic instructions compared to just 1% for standard Java methods26. Watermarks of up to 150 bits increased program size by between 40% and 75%, while performance decreased by between 0% and 36%23.

Dynamic Graph Watermarking

Collberg and Thomborson27 proposed the first dynamic graph based watermarking scheme CT to overcome problems with static watermarking schemes; most notably, static watermarks are highly fragile and therefore susceptible to semantics-preserving transformation attacks28.

Dynamic graph watermarking schemes are similar to static graph watermarking except the graph structures are built at run-time. CT can use any of the previously described graph encoding schemes to store the watermark. We would inspect the Java heap to retrieve our watermark when the program is executed with the secret input.

The first implementation29 of the CT algorithm CT_JW, implemented in a system called JavaWizz 30, was for Java bytecode using PPCT graphs to encode the watermark integer. A class is chosen from the program to be watermarked and converted into a node class by adding additional fields which contain references to other nodes.

Palsberg et al.29 discuss a simple implementation which only resists attacks against dead-code removal; they suggest that other software protection techniques are applied after the program has been watermarked. Dependencies are added between the watermark generating code and the original program by replacing a statement S with a statement of the form if(x != y) S where x and y are distinct nodes in the watermark graph.

In order to retrieve the watermark, the watermarked program is executed and the Java heap is accessed by dumping an image using the -Xhprof heap profiling JVM option31.

The following steps are performed to retrieve the watermark:

• Extracting potential node classes
• Exracting potential node objects
• Determining potential edges
• Searching for the watermark graph

In general, searching for the graph would be an NP-complete problem however we know that the graph is a PPCT graph of a certain size and can prune away unnecessary nodes. Palsberg et al.32 evaluated their implementation and found that, although it is possibly to retrieve a watermark, it is time-consuming - taking from 0.6 minutes up to 8.9 minutes on their set of test programs. It was shown that the CT algorithm is a good watermarking scheme because it is stealthy and resilient to semantics-preserving transformation attacks but it must be combined with other software protection techniques such as obfuscation33 and tamper-proofing 34.

Collberg and Thomborson4 implemented a version of the CT algorithm, CT_SM, in Sandmark 24 and compared it to JavaWiz29. The CT_SMimplementation differs from the JavaWiz in the following ways:

1. CT_SMrequires a key to encode and decode the watermark, requiring user annotation of the program to be watermarked
2. CT_SMcan encode arbitrary strings whereas CT_JW requires an integer watermark
3. CT_JW uses PPCTs to encode the watermark, whereas CT_SMoffers the choice of Radix, PPCT, Permutation or Reducible Permutation graphs; also offering a cycled graph option to protect against node-splitting attacks.
4. CT_JW's graph building code is concentrated in one location whereas CT_SMembeds code fragments at sereval user-specified locations
5. CT_JW uses an existing class for graph nodes whereas CT_SW generates its own
6. CT_JW uses the heap profiling option of the JVM whereas CT_SM uses the Java Debug Inteferace (JDI) API 35

The CT_SW algorithm embedding algorithm consists of the following steps:

• Annotation In this first step the programmer must insert calls to a method mark() which indicates to the watermarking system locations in which graph building code can be inserted. This manual annotation step allows a programmer to carefully choose the best locations for code insertion, maximising the stealthiness of the embedded watermark.
• Tracing After the code has been annotated the program is run with a secret input during which one or more annotation points will be encountered. Some of these encountered locations are used to store the graph building code.
• Embedding The watermark is encoded in a graph structure (strings watermarks are first converted to integers) and is converted into Java bytecode that builds the graph. The graph node class is generated from a similar class already in the program, or if no suitable class is found, classes from the Java library, such as LinkedList could be used. The graph is partitioned into several, equal sized, sub-graphs so that the code is more stealthy and the code is inserted at the marked locations discovered in the tracing step.

During extraction the program is run with the secret input; this will invoke the graph building code at the locations marked by the programmer. The graph structure will be on the Java heap and the Java debugging interface is used to retrieve it. The JDI is used to add breakpoints to every constructor in the program to build a circular linked buffer of the last 1000 objects allocated. The list is then searched, in reverse, for the watermark graph.

Collberg and Thomborson4 evaluate CT_SM and conclude that it is efficient and resilient to semantics-preserving transformations. The greatest vulnerability is it's limited stealthiness and it is suggest that future work investigates combining a locally stealthy but not steganographically stealthy technique, such as describe by Nagra and Thomborson36, with the CT algorithm would be helpful.

Attacks against graph watermarks

Collberg et al.4 describe 4 types of attacks against dynamic graph watermarking schemes:

• adding extra graph edges
• adding extra nodes to the graph
• renaming and re-ordering instance variables
• splitting nodes into several linked parts

However, an adversary will probably not know the location of the watermark in a large program and as such would have to apply transformations across the program resulting in a large performance decrease. The use of RPG or PPCT graphs prevent renaming and re-ordering attacks because these graph encodings do not rely on the order of the nodes.

The biggest problem is the addition of bogus nodes to a graph for which tamper-proofing techniques are required. Collberg et al.37 suggest the use of Java reflection may help. However, they did not implement this because they conclude that the code would be unstealthy as this kind of code is unusual in most programs.

Luo et al.38 describe an algorithm based on CT using the Chinese Remainder Theorem25 to split the watermark.

Tamper-proofing by Constant Encoding

He39, and later Thomborson et al.40, developed a tamper-proofing technique for dynamic graph watermark called constant encoding. Constant encoding encodes some of the constants in a program into a tree structure similar to the watermark and decodes them at run-time. An attacker cannot distinguish between the watermark graph and the constant encoding graphs so they cannot change any graph structure as they may introduce bugs into the program.

An attacker that manipulates the constant graph will change the encoding; so the decode function will return a different number and the program will be semantically incorrect.

A weakness of this system is that an attacker may be able to discover that certain program functions always return the same value, for every execution. He39 suggests introducing dependencies, to make the code harder to analyse, by providing an input variable to the decoding function. A further suggestion, for future work, is to change the constant tree at runtime making the code harder to analyse.

Jian-qi et al.41 propose using the constant encoding functions within the parameters of opaque predicates42 so that if an attacker manipulates a constant graph control will pass to the wrong clause of an if statement using the opaque predicate.

Thomborson et al.40 combine the watermarking and tamper-proofing techniques further by using sub-graphs of the watermark graph to encode constants, rather than separate graphs. Thomborson et al.40 also formally define the problem of tamper-proofing and show that commonly occurring constants in computer programs can be replaced automatically and that a long series of dynamic analyses would be required to remove the watermark. However, it is not clear if their constant encoding technique is resilient against pattern-matching attacks -- a question which is left for future work.

Khiyal et al.43 suggest splitting constants so that large constants can be encoded in small trees. They evaluated the constant encoding technique by comparing watermarked and tamper-proofed programs for efficiency, size and resilience. They found that the size of a program does increase when tamper-proofed and the execution time is slower; however, the tamper-proofing technique should be used with obfuscation to further protect a tamper-proofed program.

Conclusion

We have presented a survey of software watermarking schemes based on graph encoding using both static and dynamic embedding techniques. Static techniques, as always, are highly susceptible to semantics preserving transformation attacks and are therefore easily removed by an adversary.

Dynamic graph watermarking, however, is resilient to most semantics-preserving transformations if the right graph encoding is chosen. However, a choice between variable degrees of high stealth, resilience and bit-rate has to be made, as no algorithm has been developed which combines the best of all these properties.

Further research should continue into dynamic graph watermarking, especially on improving the CT algorithm from attacks. We intend to investigate the use of program slicing44 to attack dynamic watermarks and improve resilience to subtractive attacks.

Download the full paper which contains more details and examples.

• 1. a. b. c. Collberg, C., S. Kobourov, E. Carter, and C. Thomborson, Error-Correcting Graphs for Software Watermarking, 2003.
• 2. Ghiya, R., and L. J. Hendren, Is it a tree, a DAG, or a cyclic graph? A shape analysis for heap-directed pointers in C, St. Petersburg Beach, Florida, United States, ACM, 1996.
• 3. Ramalingam, G., "The undecidability of aliasing", ACM Trans. Program. Lang. Syst., vol. 16, pp. 1467–1471, 1994.
• 4. a. b. c. d. Collberg, C., C. Thomborson, and G. M. Townsend, "Dynamic graph-based software fingerprinting", ACM Trans. Program. Lang. Syst., vol. 29, pp. 35, 2007.
• 5. Harary, F., and E. M. Palmer, Graphical Enumeration: Academic Press, New York,, pp. xiv, 271 p., 1973.
• 6. Knuth, DE., "The art of computer programming, volume 1: fundamental algorithms", Addison-Wesley, Reading, Mass, vol. 1, 1973.
• 7. Catalan, E., "Note extraite d’une lettre adressée à l’éditeur", Journal für die reine und angewandte Mathematik, vol. 27, pp. 192, 1844.
• 8. Koshy, T., Catalan Numbers with Applications: Oxford University Press, pp. 422, 2008.
• 9. a. b. c. d. Collberg, C., and J. Nagra, Surreptitious Software: Obfuscation, Watermarking, and Tamperproofing for Software Protection: Addison-Wesley, 2009.
• 10. Chen, XJ., DY. Fang, JB. Shen, F. Chen, WB. Wang, and L. He, A Dynamic Graph Watermark Scheme of Tamper Resistance: IEEE Computer Society, 2009.
• 11. Ping, Z., C. Xi, and Y. Xu-Guang, "The Software Watermarking for Tamper Resistant Radix Dynamic Graph Coding", Inform. Technol. J., vol. 9, pp. 1236–1240, 2010.
• 12. Zhu, J., Y. Liu, and K. Yin, "A Novel Planar IPPCT Tree Structure and Characteristics Analysis", Journal of Software, vol. 5, pp. 344, 2010.
• 13. Yong, W., and Y. Yixian, "A software watermark database scheme based on PPCT", CIHW2004, 2004.
• 14. Zhu, J., K. Yin, and Y. Liu, "A Novel DGW Scheme Based on 2D\_PPCT and Permutation", Multimedia Information Networking and Security, International Conference on, vol. 2, pp. 109–113, 2009.
• 15. Jianqi, Z., L. YanHeng, Y. Ke, and Y. KeXin, "A Novel Method-Based Software Watermarking Scheme", Information Technology: New Generations, Third International Conference on, pp. 388–392, 2009.
• 16. a. b. Venkatesan, R., V. Vazirani, and S. Sinha, "A graph theoretic approach to software watermarking", Information Hiding: Springer, 2001.
• 17. a. b. Venkatesan, R., and V. Vazirani, Technique for producing, through watermarking, highly tamper-resistant executable code and resulting" watermarked" code so formed, 2004.
• 18. a. b. Aho, A. V., M. S. Lam, R. Sethi, and J. D. Ullman, Compilers: Principles, Techniques, and Tools, 2nd: Addison Wesley, pp. 796, 2006.
• 19. Hecht, M. S., and J. D. Ullman, Flow graph reducibility, Denver, Colorado, United States, ACM, 1972.
• 20. Hecht, M. S., and J. D. Ullman, "Characterizations of Reducible Flow Graphs", J. ACM, vol. 21, pp. 367–375, 1974.
• 21. Chroni, M., and S. D. Nikolopoulos, Encoding watermark integers as self-inverting permutations, Sofia, Bulgaria, ACM, 2010.
• 22. Arora, S., S. Rao, and U. Vazirani, Expander flows, geometric embeddings and graph partitioning, Chicago, IL, USA, ACM, 2004.
• 23. a. b. Collberg, C., A. Huntwork, E. Carter, and G. Townsend, "Graph Theoretic Software Watermarks: Implementation, Analysis, and Attacks", Workshop on Information Hiding, 2004.
• 24. a. b. Collberg, C., Sandmark, 2004.
• 25. a. b. Lam, L., Fleeting footsteps: tracing the conception of arithmetic and algebra in ancient China, Rev. ed., Singapore, River Edge NJ, World Scientific, 2004.
• 26. Collberg, C., A. Huntwork, E. Carter, G. Townsend, and M. Stepp, "More on graph theoretic software watermarks: Implementation, analysis, and attacks", Inf. Softw. Technol., vol. 51, pp. 56–67, 2009.
• 27. Collberg, C., "Software watermarking: Models and dynamic embeddings", Proceedings of the 26th ACM SIGPLAN-SIGACT, 1999.
• 28. Hamilton, J., and S. Danicic, "An Evaluation of Static Java Bytecode Watermarking", Proceedings of the International Conference on Computer Science and Applications (ICCSA’10), The World Congress on Engineering and Computer Science (WCECS’10), San Francisco, USA, 2010.
• 29. a. b. c. Palsberg, J., S. Krishnaswamy, M. Kwon, and D. Ma, "Experience with software watermarking", Proceedings of the 16th Annual Computer Security Applications Conference: IEEE Computer Society, 2000.
• 30. Palsberg, J., and D. Ma, Javawiz, 2000.
• 31. O'Hair, K., "HPROF: A Heap/CPU Profiling Tool in J2SE 5.0", Sun Developer Network, vol. Developer, no. 2010-08-31, 2004.
• 32. Citekey palsberg_experience_2000 not found
• 33. Collberg, C., C. Thomborson, and D. Low, A taxonomy of obfuscating transformations, 1997.
• 34. Collberg, CS., and C. Thomborson, "Watermarking, tamper-proofing, and obfuscation-tools for software protection", Software Engineering, IEEE łdots, vol. 28, pp. 735–746, 2002.
• 35. Microsystems, I. Sun, Java Debug Interface, 2005.
• 36. Nagra, J., and C. Thomborson, "Threading Software Watermarks", Lecture Notes in Computer Science: Springer, 2004.
• 37. Citekey collberg_dynamic_2007 not found
• 38. Luo, Y-X., J-H. Cheng, and D-Y. Fang, Dynamic Graph Watermark Algorithm Based on the Threshold Scheme: IEEE Computer Society, 2008.
• 39. a. b. He, Y., Tamperproofing a Software Watermark by Encoding Constants, 2002.
• 40. a. b. c. Thomborson, C., J. Nagra, R. Somaraju, and C. He, Tamper-proofing software watermarks, Darlinghurst, Australia, Australia, Australian Computer Society, Inc., 2004.
• 41. Jian-qi, Z., W. Ai-min, and L. Yan-heng, "Tamper-proofing Software Watermarking Scheme Based on Constant Encoding", Education Technology and Computer Science, International Workshop on, vol. 1, pp. 129–132, 2010.
• 42. Collberg, C., C. Thomborson, and D. Low, "Manufacturing Cheap, Resilient, and Stealthy Opaque Constructs", Proceedings of the 25th ACM SIGPLAN-SIGACT symposium on Principles of programming languages: ACM, 1998.
• 43. Khiyal, M. Sikandar H., A. Khan, S. Amjad, and S. M. Khalil, "Evaluating Effectiveness of Tamper Proofing on Dynamic Graph Software Watermarks", CoRR, vol. abs/1001.1, 2010.
• 44. Weiser, M., "Program slicing", Proceedings of the 5th international conference on Software engineering, Piscataway, NJ, USA, IEEE Press, 1981.