I've recently been working on visualising program slices using graphs.

I currently have 5 types of graphs:

1. Slicing criterion graph: x is connected to everything in the slice(x)
2. Maximal slice graph: if x generates a maximal slice, x is connected to everything in the slice(x). x is a crucial point.
3. Slice subest ordering graph: x is connected to y if slice(x) \( \subseteq \) slice(y) such that there is no z where slice(z) \( \subseteq \) slice(y)
4. Transitive closure of (3)
5. Clump graph: intersecting maximal slices are grouped together

Here's some examples of the graphs - they were created from the standard test jar that accompanies Sandmark, a tic-tac-toe application. Actually, it's 3 programs: a Swing application, an applet and a command line application. Each application is completely separate; the first 2 have only 1 class (+ a few annonymous classes) while the command line application uses 3 classes. Crucial points are coloured; nodes are sized relative to their number of edges. The graphs use the Fruchterman-Reingold layout algorithm which produces some nice looking graphs. I'm using Indus to slice the programs and the Gephi toolkit to create the graphs.

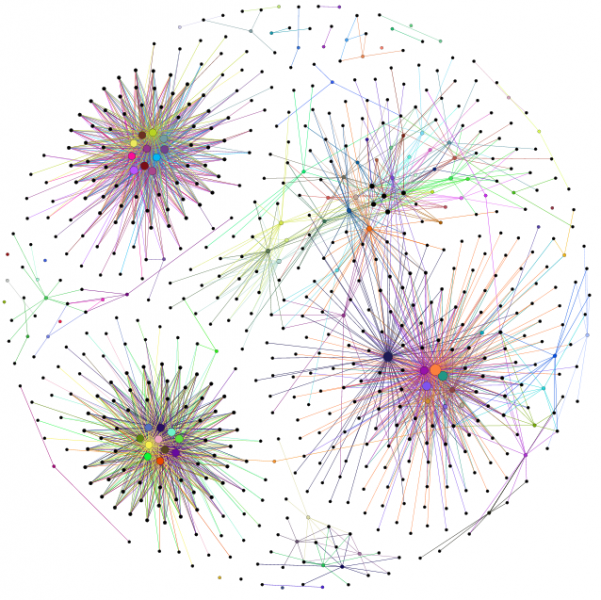
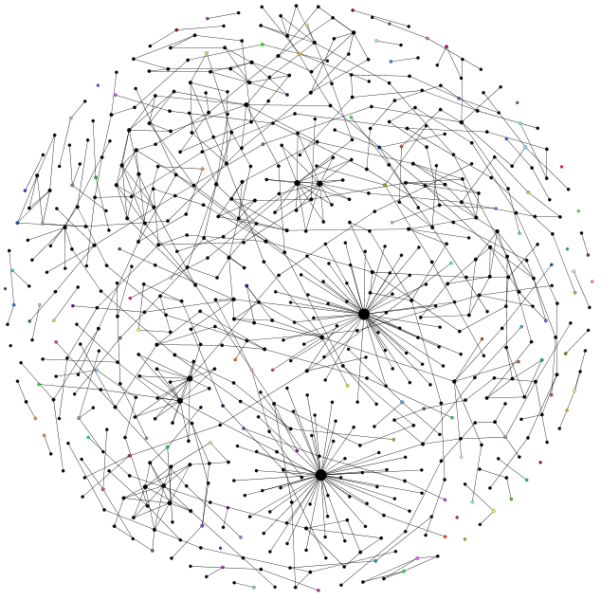
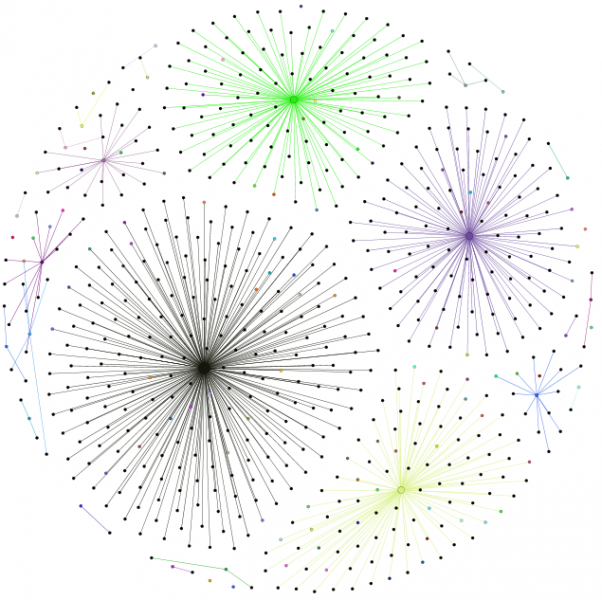
The reason that I'm doing this is to find vulnerabilities in watermarks. Are watermarks inherently unstealthy? Can program slicing reveal their location? If it can, how can we improve watermarking?

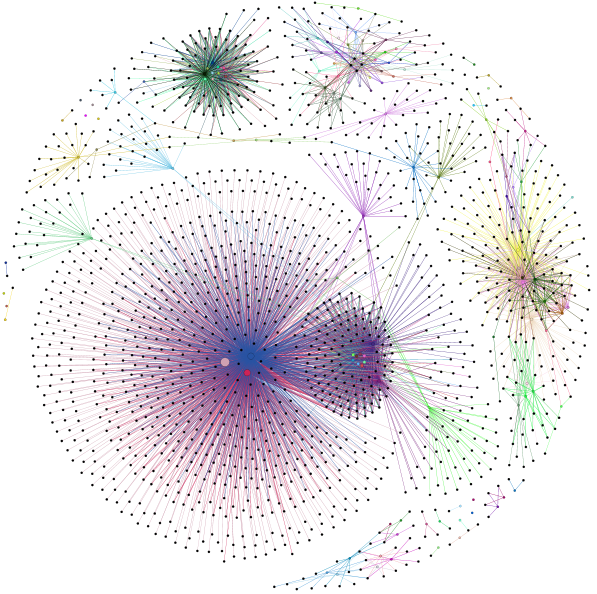
The watermarks are not completely separate from the original program due to the use of opaque predicates - these use variables from the original program to 'connect' the watermark to the program. It's not clear yet whether all watermarks can be detected easily but, intuitively, it seems that watermarks might be separate communities within a program slice graph - the watermark code would be highly connected to itself but less so with the rest of the program. This is still a work in progress; more coming soon...